SARESP

Fonte das Imagens: SED

Resolução SE 59, de 27-09-2018 - Dispõe sobre a aplicação de provas relativas ao ...

... Sistema de Avaliação de Rendimento Escolar do Estado de São Paulo - SARESP/2018

... A avaliação do SARESP deverá se realizar nos dias 27 e 28-11-2018... 

SARESP2018

27/11/2018 e 28/11/2018

Em 2017, nos dias 08 e 09 de novembro, o SARESP avaliará o desempenho dos alunos do 3º, 5º, 7º (amostral para a rede estadual) e 9º anos do Ensino Fundamental e da 3ª série do Ensino Médio, do ensino regular da rede estadual e das demais redes que aderirem à avaliação. Os alunos farão provas de Língua Portuguesa e Matemática. 

Questões do Relatório Pedagógico 2015

https://drive.google.com/file/d/0B65xmAIB-Kr6Ymk3bTYxWHBaLTQ/view?usp=sharing

Fazendo análises referentes ao SARESP/2015

Quinto Ano – Ensino Fundamental

Página 108 – Exemplo 5.5¹⁰

H13 – Resolver problemas que envolvam a multiplicação e a divisão, especialmente em situações relacionadas à comparação entre razões e à configuração retangular.

Um automóvel gasta 10 litros de gasolina a cada 80 quilômetros. Quantos litros de gasolina esse automóvel gastará se percorrer 160 quilômetros?

(A) 15.

(B) 20.

(C) 25.

(D) 30.

Observações:

·         Percentuais de Acertos: 61,60 (B)

·         10 (expoente) Compõe a descrição do ponto 225 da Escala de Proficiência de Matemática – SARESP

·         Ideia de Proporcionalidade

·         Nível Adequado: 225 A < 275

·         Página 225 – Resolvem problema envolvendo as quatro operações fundamentais e seus principais significados, envolvendo números naturais.

Fonte: Relatório Pedagógico 2015 - SARESP

Matemática – Página 68

H13 – GIII (Competências para compreender) – Competência de Área 1 (Desenvolver o raciocínio quantitativo e o pensamento funcional, isto é, o pensamento em termos de relações e a variedade de suas representações, incluindo as simbólicas, as algébricas, as gráficas, as tabulares e as geométricas). – Tema 1 (Números, operações, funções).  

Fonte: Matriz de Referência para Avaliação do SARESP

Analisando Questões do SARESP/2015 - EF II

Sétimo Ano – Ensino Fundamental

Página 125 – Exemplo 7.1¹⁴

H17 – Classificar formas planas e espaciais.

Observe as figuras. 

Essas figuras são classificadas, respectivamente, como:

(A) cone e quadrado.

(B) prisma e retângulo.

(C) triângulo e pirâmide.

(D) triângulo e cubo.

Observações:

·         Percentuais de Acertos: 82,80

·         Objetivo: investigar a classificação de uma figura plana e outra espacial.

·         14 (expoente) Compõe a descrição do ponto 175 da Escala de Proficiência de Matemática – SARESP

·         Nível Abaixo do Básico: < 200

·         Localizei a descrição no ponto 225 da Escala de Proficiência – Distinguem figuras planas de figuras espaciais (Sétimo Ano) – página 232   

Fonte: Relatório Pedagógico 2015 - SARESP

Matemática – Página 75

H17 – GII (Competências para realizar) – Competência de Área 2 (Compreender as propriedades dos objetos e a sua posição relativa e desenvolver o raciocínio espacial por meio de construções e de  formas.). – Tema 2 (Espaço e forma). 

Fonte: Matriz de Referência para Avaliação do SARESP

Questões SARESP e Plataforma Foco Aprendizagem

https://drive.google.com/file/d/0B65xmAIB-Kr6aHNnN0pwd1JQdGs/view?usp=sharing

Questões do EM/SARESP

https://drive.google.com/file/d/0B65xmAIB-Kr6RW9pc3FLSUR0NFU/view?usp=sharing

Questões do Nono Ano/SARESP

https://drive.google.com/file/d/0B65xmAIB-Kr6VTI0QWFjV1JTXzA/view?usp=sharing

Questões do Sétimo Ano/SARESP

https://drive.google.com/file/d/0B65xmAIB-Kr6dkZSRDMxdWFsSEU/view?usp=sharing

 

SARESP 2015 - Quinto Ano

H05 - Identificar a localização de números racionais representados na forma decimal na reta numérica. 

 Os pontos A, B, C e D marcados na reta numérica representam os números 

(A) 0,1; 1,6; 2,0; 3,1. 

(B) 0,1; 1,6; 2,0; 3,0. 

(C) 0,1; 1,7; 2,1; 3,0. 

(D) 0,1; 1,7; 2,1; 3,1. 

Nível Avançado: ≥ 275

Observação: Compõe a descrição do ponto 275 da Escala de Proficiência de Matemática - SARESP.

Matriz de Referência para Avaliação do SARESP - H05 - Tema 1 - Números, operações, funções - Competência de Área 1 - Grupo I - Competências para Observar. 

Anexos - página 179 - 175 á 275 - Pontos da Escala de Proficiência. 

SARESP 2015 - Quinto Ano

H13 - Resolver problemas que envolvam a multiplicação e a divisão, especialmente em situações relacionadas à comparação entre razões e à configuração retangular. 

Uma granja tem 300 ovos para embalar em bandejas do tipo mostrado na figura. 

O número de bandejas necessárias para embalar todos os ovos é: 

(A) 30.

(B) 20. 

(C) 10. 

(D) 5. 

Nível Avançado: ≥ 275

Observação: Compõe a descrição do ponto 275 da Escala de Proficiência de Matemática - SARESP. 

Matriz de Referência para Avaliação do SARESP - Matemática - Quarta Série - AF - GIII - Competências para compreender - Tema 1 - Números, operações, funções - Competência de Área 1 - página 68. 

Anexos - H13 - 175 á 275 - página 179.    

SARESP 2015 - Quinto Ano

H02 - Relacionar a escrita numérica às regras do sistema posicional de numeração. 

Henrique escreveu durante uma atividade um número formado por 45 unidades de milhar e 38 unidades. 

O número escrito por Henrique foi 

(A) 4538. 

(B) 45308. 

(C) 45038. 

(D) 450038.  

Nível Adequado: 225 A < 275

Observação: Compõe a descrição do ponto 250 da Escala de Proficiência de Matemática - SARESP. 

Matriz de Referência para Avaliação do SARESP - Matemática - Quarta Série - AF - página 68 - Grupo II - Competências para Realizar - Tema 1 - Números, operações, funções - Competência de Área 1. 

Anexos - página 179 - 175 à 300.  

SARESP 2015 - Quinto Ano

H13 - Resolver problemas que envolvam a multiplicação e a divisão, especialmente em situações relacionadas à comparação entre razões e à configuração retangular.    

Renato colheu 1.530 quilogramas de laranjas e quer colocá-las em sacos, cada um com 18 quilogramas de laranjas. 

Para ensacar todas as laranjas, ele vai precisar de 

(A) 58 sacos. 

(B) 64 sacos.      

(C) 72 sacos. 

(D) 85 sacos.        

Nível Adequado: 225 A < 275

Observação: Compõe a descrição do ponto 250 da Escala de Proficiência de Matemática - SARESP. 

Matriz de Referência para Avaliação do SARESP - Quarta Série do AF - página 68 - GIII - Competência para compreender - Tema 1 - Números, operações, funções - Competência de Área 1. 

Anexos - H13 - 175 - 200 - 225 - 250 e 275 - página 179

SARESP 2015 - Quinto Ano

H12 - Resolver problemas que envolvam a adição ou a subtração, em situações relacionados aos seus diversos significados.  

Fávio comprou um caderno de 200 folhas. Ele já usou 104 folhas desse caderno. Quantas folhas, sem uso, ainda restam no caderno de Flávio? 

(A) 96. 

(B) 104. 

(C) 106. 

(D) 304. 

Percentuais de Acertos: 72,8. 

Nível Básico: 175 A < 225

Observação: Compõe a descrição do ponto 200 da Escala de Proficiência de Matemática - SARESP. 

Anexos - H12 - Pontos da Escala de Proficiência - 175, 200 e 225 - página 179 do Relatório Pedagógico 2014.

Matriz de Referência para Avaliação do SARESP - página 68 - Tema 1 - Números, operações, funções - Grupo III - Competências para Compreender.  

SARESP 2015 - Quinto Ano

H29 - Ler e/ou interpretar informações e dados apresentados em tabelas e construir tabelas. João e Maria colecionam selos e figurinhas e anotam a quantidade que têm no quadro a seguir:  

	Quantidade de Figurinhas	Quantidade de Selos
João	86	54
Maria	78	67

O número de selos de João é igual a: 

(A) 54. 

(B) 67. 

(C) 78. 

(D) 86. 

Percentuais de Acertos: 82,7

Observação: Compõe a descrição do ponto 175 da Escala de Proficiência de Matemática - SARESP. 

Anexos - página 179 - Pontos: 175, 200, 225, 250 e 275. 

Matriz de Referência: Quarta Série - página 67 - Grupo III - Competências para Compreender - Tema 4 - Tratamento da Informação.   

SARESP 2015 - Quinto Ano

H22 - Reconhecer unidades de medida usuais de comprimento, de superfície, de capacidade, de tempo e de temperatura.

Desconfiada de uma possível febre, a mãe de Pedro mediu a sua temperatura obtendo a leitura abaixo.     

Nível Básico: 175 A < 225

Percentuais de Acertos: 85,2

Anexos - página 179 -  < 150, 175 e 200.

Matriz de Referência - página 69 - Competência de Área 3 - Tema 3 - Grandezas e Medidas - Grupo I - Competência de Observar.    

Observação: Compõe a descrição do ponto 175 da Escala de Proficiência de Matemática - SARESP 

Fonte: Relatório Pedagógico 2014  

SARESP 2015 - Quinto Ano

H08 - Identificar sequências numéricas. 

Observação: compõe a descrição do ponto 150 da Escala de Proficiência de Matemática - SARESP. O intervalo de um desvio padrão garante que a maioria dos alunos está sendo levada em consideração. 

Nível Abaixo do Básico: < 175

Matriz de Referência para Avaliação do SARESP - Matemática - Quarta Série do Ensino Fundamental 

Grupo GI - Competências para observar 

Tema 1 - Números, operações, funções. 

Competência de Área 1

Anexos - Relatório Pedagógico 2014 - pontos: 150, 175, 200 e 250 na Escala de Proficiência.

Fonte: Relatório Pedagógico 2014

Números Naturais/SARESP

Reta Numérica

H01 - Identificar a localização de números naturais na reta numérica. 

A distância entre a casa de Elias e sua escola é de 20 km. Para ir até a escola, ele passa por uma igreja. 

A igreja está localizada no quilômetro: 

a) 10

b) 12 

c) 14

d) 16 

SARESP 2012

1.  A despesa de Quitéria no Armarinho Pague e Leve foi de R$ 18,70. Ela comprou uma cartela de agulhas, uma cartela de botões e três tesouras.

 AGULHAS = R$ 2,60 e BOTÕES = R$ 3,20.

O preço de cada tesoura é:

A)   R$ 4,30.

B)   R$ 5,80.

C)   R$ 6,23.

D)   R$ 8,60.

SARESP 2015 - Sétimo Ano

H25 - Efetuar cálculos que envolvam medidas de ângulos.

Observação: compõe a descrição do ponto 300 da Escala de Proficiência de Matemática - SARESP

Grupo II - Competências de Realizar

Competência de Área 3

Tema 3 - Grandezas e Medidas

Consultar o ANEXO da página 187, níveis: 250, 275, 300 e 325.

Tema 3 - Grandezas e Medidas - Reconhecer, Determinar e Resolver.

Nível Avançado: ≥ 300

Fonte: Relatório Pedagógico 2014

SARESP 2015 - Sétimo Ano

H13 - Aplicar uma ordem de operações ao resolver problemas (parênteses, multiplicação, divisão, adição e subtração).

Se adicionarmos 3 ao dobro da idade de Ana, vamos obter a minha idade, ou seja, 37 anos. Quanto anos Ana Tem? 

(A) 17 anos. 

(B) 34 anos. 

(C) 40 anos. 

(D) 77 anos. 

Nível Avançado: ≥ 300

Matriz de Referência para Avaliação do SARESP - Matemática - Sexta Série do EF AF  

Tema 1 - Números, operações, funções, iniciação à Álgebra. 

Competência de Área 1  

GIII - Competências para compreender 

Fonte: Relatório Pedagógico 2014

SARESP 2015 - Sétimo Ano

H22 - Realizar medidas usando padrões e unidades não convencionais ou de outros sistemas de medidas.

João, Laura, Tales e Cristina são primos e, numa brincadeira, mediram o comprimento da varanda da casa da avó, utilizando cada um o seu próprio pé como unidade de comprimento. O resultado da medição feita por João foi de 40 pés, o de Laura 56 pés, o de Tales 42 pés e o de Cristina 48 pés. 

Desta forma, quem tem o pé com maior comprimento é: 

(A) João. 

(B) Laura. 

(C) Tales. 

(D) Cristina. 

Observação: compõe a descrição do ponto 275 da Escala de Proficiência de Matemática - SARESP. 

Anexos, página 187, pontos: 200, 225, 250, 275 e 300. No ponto 275 - Tema 3 - Grandezas e Medidas - Determinam dentre quatro pessoas aquela que possui o maior pé, dado a quantidade de pés que cada um utilizou para medir uma mesma distância. 

Competência de Área 3 

Nível Adequado: 250 A < 300 

Fonte: Relatório Pedagógico 2014  

SARESP 2015 - Sétimo Ano

H08 - Compreender a relação entre as representações fracionária e decimal de um número. 

Observação: compõe a descrição do ponto 275 da Escala de Proficiência de Matemática - SARESP

Grupo: GI

Tema: números, operações, funções, iniciação à Álgebra. 

Competência de Área 1  

Nível Adequado: 250 A < 300 

Ponto 275 - Tema 1 - Aritmética e Álgebra - Identificam a moeda que equivale a 1/4 de real. 

Fonte: Relatório Pedagógico 2014

SARESP 2015 - Sétimo Ano

H01 - Reconhecer as principais características do sistema decimal: contagem, base, valor posicional

No número 3.457, o algarismo com maior valor posicional é o:

(A) 3.

(B) 4.

(C) 5.

(D) 7. 

Observação: compõe a descrição do ponto 250 da Escala de Proficiência de Matemática - SARESP.

Nível Adequado: 250 A < 300 

Consultar a Matriz de Referência para a Avaliação SARESP - GI - Competências para Observar - Tema 1: números, operações, funções, iniciação à álgebra - Competência de Área 1 - Desenvolver o raciocínio quantitativo e o pensamento funcional, isto é, o pensamento em termos de relações e a variedade de suas representações, incluindo as simbólicas, as algébricas, as gráficas, as tabulares e as geométricas. Aplicar expressões analíticas para modelar e resolver problemas.    

SARESP 2015 - Sétimo Ano

H35 - Identificar e interpretar informações transmitidas por meio de gráficos. (GIII)

A principal modalidade de transporte coletivo na Capital e na Grande São Paulo atraiu menos passageiros nos últimos cinco anos, como mostram os gráficos a seguir: 

A respeito das informações do texto e do gráfico, é correto afirmar que a quantidade de passageiros de

(A) metro aumentou; trem aumentou; ônibus metropolitano não foi alterada e de ônibus municipal não foi alterada. 

(B) metro aumentou; trem aumentou; ônibus metropolitano diminuiu e de ônibus municipal diminuiu. 

(C) metro aumentou; trem não foi alterada; ônibus metropolitano não foi alterada e de ônibus municipal diminuiu. 

(D) metro aumentou; trem aumentou; ônibus metropolitano não foi alterada e de ônibus municipal diminuiu.  

Observação: compõe a descrição do ponto 225 da Escala de Proficiência de Matemática - SARESP. 

Nível Básico: 200 A < 250

Competência de Área 4 - Tema 4 

Grupo III - Competências para compreender  

SARESP 2015 - Sétimo Ano

H15 - Expressar e resolver problemas por meio de equações.

A professora colocou o seguinte desafio:

- Pensei em um número. - Multipliquei por 12. - Somei 10 ao resultado, obtendo 58. - Em qual número eu pensei?

Júlia resolveu corretamente o desafio, obtendo o número:

(A) 1.

(B) 2.

(C) 3.

(D) 4.

Observação: compõe a descrição do ponto 225 da Escala de Proficiência de Matemática - SARESP.

Nível Básico: 200 A < 250

Sétimo Ano do Ensino Fundamental 

Fonte: Relatório Pedagógico 2014 - SARESP.

SARESP/SÉTIMO ANO

Habilidade Avaliada 

H18 - Identificar figuras espaciais a partir de suas planificações. (GI)

Das figuras seguintes, aquela que representa a planificação de um cubo é: 

SARESP/SÉTIMO ANO

Habilidade Avaliada 

H21 - Identificar elementos e classificar poliedros. (GII)

O número de arestas do prisma pentagonal é: 

(A) 5.

(B) 9.

(C) 12.

(D) 15.

SARESP 2015 - Nono Ano

H03 - Reconhecer as representações decimais dos números racionais como uma extensão do sistema de numeração decimal, identificando a existência de "ordens" como décimos, centésimos e milésimos.   

Se colocados em ordem crescente os números decimais 0,05 - 0,5 - 0,003 - 0,057 - 0,35 têm-se 

(A) 0,05 - 0,5 - 0,003 - 0,057 - 0,35. 

(B) 0,003 - 0,05 - 0,057 - 0,35 - 0,5. 

(C) 0,003 - 0,05 - 0,057 - 0,5 - 0,35. 

(D) 0,5 - 0,35 - 0,057 - 0,05 - 0,003. 

Nível Avançado:  ≥  350

Observação: compõe a descrição do ponto 350 da Escala de Proficiência de Matemática - SARESP  

Fonte: Relatório Pedagógico 2014 - SARESP 

SARESP 2015 - Nono Ano

H05 - Identificar a expressão algébrica uma regularidade observada em sequência de números ou figuras (padrões). 

As variáveis x e n assumem valores conforme tabela abaixo. 

x	2	4	6	8	10
n	4	8	12	16	20

Nível Adequado: 300 < 350

A relação x e n é dada pela expressão

(A) n = x + 2. 

(B) n = 2x. 

(C) n = 2x + 2. 

(D) n = x + 4.

Observação: compõe a descrição do ponto 325 da Escala de Proficiência de Matemática -SARESP

Fonte: Relatório Pedagógico 2014 SARESP

SARESP 2014

Exemplo 5²⁹

H03 - Resolver problemas com números racionais que envolvam as operações (adição, subtração, multiplicação, divisão, potenciação e radiciação). 

Estou planejando uma viagem de automóvel. O consumo do veículo é de 10 km/L e o preço do combustível é de R$ 2,00. Se a distância que irei percorrer é de 420 km e o pedágio custa R$ 67,10, o valor que gastarei só para é:

(A)      R$ 96,25.

(B)       R$ 102,75.

(C)       R$ 136,40.

(D)      R$ 151,10.

Percentuais de Acertos: (D) 40,3.

Compõe a descrição do ponto 300 da Escala de Proficiência de Matemática – SARESP

SARESP 2012

AS FIGURAS PINTADAS CORRESPONDEM RESPECTIVAMENTE AS REPRESENTAÇÕES FRACIONÁRIAS DE: 

A) 7/9, 7/12 e 7/11;
B) 6/9, 7/12 e 6/11;
C) 7/9, 7/12 e 7/11;
D) 6/9, 6/12 e 7/11.


OBSERVAÇÃO: AS PARTES SÃO EXATAMENTE IGUAIS.

SARESP 2014 - Relatório

H01 - Reconhecer diferentes representações de um número racional. 

Observação: espera-se desses alunos as habilidades dos anos anteriores, e ainda a capacidade de:

Identificar:

- a expressão que define o termo geral de uma sequência;
- um objeto por meio das suas vistas superior e lateral.

Aplicar o teorema de Tales.

Calcular:

- valores aproximados de radicais;
- o resultado de uma expressão dado os valores das variáveis envolvidas.

Realizar soma dos polinômios.

Resolver problemas envolvendo:

- compra e venda, descontos, lucros e prejuízos e aumentos dados em percentuais;
- cálculo de medida de comprimento de um dos lados de triângulos semelhantes;
- cálculo do perímetro de uma circunferência;
- cálculo de probabilidade simples;
- sistemas lineares de duas equações e duas incógnitas.

Compõe a descrição do ponto 300 da Escala de Proficiência de Matemática - SARESP

Percentuais de Acertos: C - 41,1

Nível Adequado: 300 A < 350

Observar os ANEXOS, página 199 e 200.

Por qual número devemos multiplicar o numerador e o denominador para encontrarmos a fração equivalente 8/20?   

Fonte: Relatório Pedagógico 2014

Nível Abaixo do Básico: < 200 - SARESP 2014

H34 – Identificar e interpretar informações transmitidas por meio de tabelas.

Destas cidades, as que possuem os mesmos DDD são:

(A)   Campinas e São Paulo.

(B)   Araquara e Santos.

(C)   Cubatão e São José do Rio Preto.

(D)   Cubatão e Santos

Observações: compõe a descrição do ponto 175 da Escala de Proficiência de Matemática – SARESP.

Percentuais de Acertos: 80,9 (página 84)

Fonte: Relatório Pedagógico do SARESP 2014

Nível Abaixo do Básico: < 225 - SARESP 2014

H22 – Identificar a localização/movimentação de objeto em mapas, croquis e outras representações gráficas.

Paula mora em Sorocaba, na região indicada pela letra P, e sua amiga Mara mora em Marília, na região indicada pela letra M, conforme mostra o mapa.

A localização das residências de Paula e Mara pode ser dada, respectivamente por:

Percentuais de Acertos: 81,5%.

Compõe a descrição do ponto 200 da Escala de Proficiência de Matemática – SARESP.

Fonte: Relatório Pedagógico 2014

Nível Básico: 225 A < 300 - SARESP 2014

H40 – Resolver problemas que envolvam noções de volume.

Compõe a descrição do ponto 225 da Escala de Proficiência de Matemática – SARESP.

Percentuais de Acertos: 79,7%.

H20 – Resolver problemas envolvendo relações de proporcionalidade direta entre duas grandezas por meio de funções do 1° grau.

Uma máquina fabrica 5 (cinco) peças a cada 6 (seis) segundos. Mantendo esse ritmo de produção, quantas peças serão produzidas em 1 (um) minuto?

(A)   20.

(B)   40.

(C)   50.

(D)  60.

Compõe a descrição do ponto 275 da Escala de Proficiência de Matemática – SARESP.

Percentuais de Acertos: 55,6%.    

Fonte: Relatório 2014 

SARESP - Geometria

Relatório 2009/SARESP

4º. Série/5º. Ano

3º. GEOMETRIA PLANA

Nível Básico: Entre 175 e 225 (≥ 175 A < 225).

Habilidade Avaliada: H19 – Identificar semelhanças e diferenças entre polígonos, usando critérios como número de lados, números de ângulos, eixos de simetria e rigidez, sem o uso obrigatório de terminologia convencional.

Observe as figuras abaixo.

As figuras que têm quatro ângulos internos são:

a)     M e N.

b)    N e P.

c)     N e Q.

d)    P e Q.

Resultados: 68,8%, aproximadamente 69%.

Relatório 2009/SARESP

4º. Série/5º. Ano

Nível Básico: Entre 175 e 225 (≥ 175 A < 225).

Habilidade Avaliada: H19 – Identificar semelhanças e diferenças entre polígonos, usando critérios como número de lados, números de ângulos, eixos de simetria e rigidez, sem o uso obrigatório de terminologia convencional.

Dos polígonos abaixo, os que possuem o mesmo número de lados são:

a)     I e II.

b)    I e III.

c)     II e IV.

d)    II e III.

Resultados: 68,8%, aproximadamente 69%.

Relatório 2010/SARESP

6º. Série/7º. Ano

Habilidade Avaliada: H17 – Classificar formas planas e espaciais.

Dentre os mosaicos abaixo, aquele que é formado somente por quadriláteros é:

Resultados: 25% dos alunos acertaram.

Relatório 2010/SARESP

6º. Série/7º. Ano

Nível Avançado: ≥ 300.

Habilidade Avaliada: H26 – Identificar a somas das medidas dos ângulos de um triângulo (180°) e de um polígono de n lados (por decomposição em triângulos).

22º.) Todos os polígonos abaixo foram montado como triângulos. Dessa forma, aquele cuja a soma das medidas dos ângulos internos é igual a 540° é:

Resultado: 21% de acertos.

SARESP

Habilidade Avaliada: H06 – Identificar um sistema de equações do 1º. Grau que expressa um problema.

Numa gincana de Matemática, Hélio calculou mentalmente dois números de modo que sua soma fosse igual a 12 e a sua diferença 2. Lúcia utilizou outra estratégia, determinando esses dois números algebricamente. Dessa forma, um possível sistema de equações para indicar o raciocínio de Lúcia é:

a)      x + y = 12 e 2.x + 3.y =1   

b)      2.x – y = 9 e 4.x + 3.y = 10

c)       x – y = 5 e x + y = 7

d)      x + y = 12 e x – y = 2

Observação: trata-se de um problema de linguagem matemática, aproximadamente (58%) dos alunos mostram esta habilidade em um problema simples envolvendo um sistema de equações. É pequeno esse percentual de acerto, se observamos o nível de dificuldade da questão e a série/ano considerada. Não é possível uma análise consistente sobre os prováveis erros cometidos pelos alunos que marcaram os distratores.

Nível Básico: Entre 225 e 300 (≥ 225 A ˂  300)    

SARESP

Habilidade Avaliada: H44 – Resolver problemas que envolvam processos de contagem; princípio multiplicativo.

4º.) Para ingressar na sala segura  de um laboratório, Mauro deve apertar 5 botões coloridos (vermelho, azul, amarelo, verde e rosa) na sequência correta. Mauro esqueceu-se da senha, mas lembrou que o primeiro botão a ser apertado era o de cor azul e o último a ser apertado era da cor verde.

Qual é o número máximo de tentativas que Mauro deve fazer para acessar a sala, sabendo que cada cor é apertada uma única vez?

a)      120

b)      30

c)       12

d)      6

SARESP/9º. ANO

Habilidade Avaliada: H30 – Resolver problemas em diferentes contextos, envolvendo triângulos semelhantes.

  

1º.) Na figura abaixo há dois triângulos semelhantes. As figuras não estão desenhadas em escala.

A medida do lado DE é:

a)      5,6 cm.

b)      8 cm.

c)      4,5 cm.

d)      3 cm.

Nível Adequado: 300 a ˂ 350.

SARESP/NONO ANO

H29 - Resolver problemas que utilizam propriedades dos polígonos (soma dos ângulos internos, número de diagonais, cálculo da medida de cada ângulo interno nos polígonos regulares).

No polígono apresentado na figura, o ângulo D mede: 

(A) 90 graus. 

(B) 80 graus.      

(C) 70 graus. 

(D) 60 graus. 

Observação: 

"A soma da medida dos ângulos internos de um polígono convexo de n lados é igual a (n-2).180°"

O polígono do problema é convexo e tem 5 lados - a medida dos seus ângulos internos é dada por 3 x 180° = 540°.

Isto significa que:

130° + 130° + 110° + 110° + medida de D = 540°

Portanto D = 540° - 480° = 60°.

SARESP/Relatório 2010

Habilidade Avaliada – H11 Efetuar cálculos simples com valores aproximados de radicais.    

10º.) Para ir do ponto A (vértice do quadrado) ao ponto B (vértice oposto) tomar um lanche, Carlos calculou que deverá andar (raiz quadrada de 1800 m). Isso quer dizer que deverá caminhar mais de: 

a)      41 m.

b)      48 m.

c)      50 m.

d)      60 m.

Observações: Tome um quadrado de 30 m x 30 m e considere a raiz quadrada de 2 como aproximadamente 1,4.   

Nível Avançado: ≥ 350.  

SARESP/REFLETIR

SARESP/2011

OBSERVANDO O EXEMPLO 14¹⁴ DA PÁGINA 86 DO 5º. ANO

14 DESCREVE O PONTO 275 DA ESCALA DE PROFICIÊNCIA DE MATEMÁTICA – SARESP 2011.

NÍVEL AVANÇADO: ≥ 275

ONDE O PERCENTUAL DE ALUNOS DA REDE ESTADUAL É DE: 9,6%.

HABILIDADE AVALIADA – H13 – RESOLVER PROBLEMAS COM NÚMEROS NATURAIS DE DOIS ALGARISMOS, ENVOLVENDO A MULTIPLICAÇÃO (MEDIDA DE TRÊS ÂNGULOS IGUAIS). (GIII)

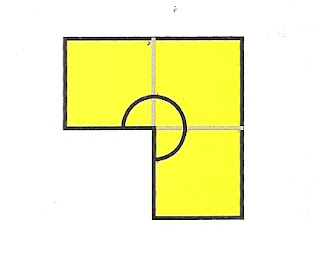
PIERRE VAI FAZER ALGUMAS BANDEIRINHAS PARA SUA FESTA. A FIGURA REPRESENTA O MOLDE DESSA BANDEIRINHA. VEJA, ELA É COMPOSTA POR TRÊS QUADRADOS.

LEMBRANDO QUE O QUADRADO TEM QUATRO ÂNGULOS DE 90⁰, A MEDIDA DO ÃNGULO ASSINALADO NA BANDEIRINHA É IGUAL A:

(A) 90⁰

(B) 135⁰

(C) 180⁰

(D)  270⁰

  

GAB: GABARITO – ALTERNATIVA CORRETA;

DIF: ÍNDICE DE DIFICULDADE, MEDIDO PELO PERCENTUAL DE ALUNOS QUE NÃO RESPONDERAM CORRETAMENTE A QUESTÃO.

O QUE OBSERVAMOS NESTA QUESTÃO?

37% DOS ALUNOS ACERTARAM A QUESTÃO E 63% DOS ALUNOS ERRARAM ESTA QUESTÃO. 

37,2 (0,2 QUE CORRESPONDE A DOIS DÉCIMOS; 0,2 < 0,5 E DEVEMOS ENTÃO CONSIDERAR O INTEIRO, 37). 37% + 63% = 100%. SI (SISTEMA INTERNACIONAL).

DISC: ÍNDICE DE DISCRIMINAÇÃO. PARA SER CONSIDERADA APTA A AVALIAR OS ALUNOS, UMAQUESTÃO DEVE SER MAIS ACERTADA POR ALUNOS QUE TIVERAM BOM DESEMPENHO DO QUE PELOS QUE TIVERAM DESEMPENHO RUIM.   QUANTO MAIOR, MELHOR É O SEU PODER DE DISCRIÇÃO.

O QUE OBSERVAMOS COM RELAÇÃO AOS ÍNDICES DE DISCRIÇÃO?

TEMOS PERCENTUAIS ALTOS DE ALUNOS DE MELHOR DESEMPENHO NA PROVA MARCANDO OS DISTRATORES.

O GRÁFICO REFERENTE À ALTERNATIVA CORRETA É CRESCENTE.

GRÁFICO DE QUANTIS, MOSTRA A PROPORÇÃO DE ALUNOS QUE ASSINALARAM CADA ALTERNATIVA, PARA 7 GRUPOS CONSECUTIVOS DOS ALUNOS, DEFINIDOS PELOS RESULTADOS DE SEUS DESEMPENHOS E CONSTRUÍDOS A PARTIR DO GRUPO DE ALUNOS DE MENOR PONTUAÇÃO, PASSANDO PELO GRUPO COM PONTUAÇÃO INTERMEDIÁRIA, ATÉ O GRUPO DOS QUE TIVEREM MELHOR DESEMPENHO NA PROVA.

DEVE-SE OBSERVAR SE A LINHA RELATIVA À ALTERNATIVA CORRETA É CRESCENTE, O QUE SIGNIFICA QUE OS ALUNOS DE MELHOR PONTUAÇÃO TENDEM A RESPONDER CORRETAMENTE COM MAIOR FREQUÊNCIA. ESPERA-SE QUE AS LINHAS RELATIVAS ÀS ALTERNATIVAS INCORRETAS (DISTRATORES) TENHAM INCLINAÇÃO NEGATIVA COMO É ESPERADO.  

Fonte: Relatório 2011.    

OBSERVANDO O EXEMPLO 14¹⁴ DA PÁGINA 86 DO 5º. ANO

14 DESCREVE O PONTO 275 DA ESCALA DE PROFICIÊNCIA DE MATEMÁTICA – SARESP 2011.

NÍVEL AVANÇADO: ≥ 275

ONDE O PERCENTUAL DE ALUNOS DA REDE ESTADUAL É DE: 9,6%.

HABILIDADE AVALIADA – H13 – RESOLVER PROBLEMAS COM NÚMEROS NATURAIS DE DOIS ALGARISMOS, ENVOLVENDO A MULTIPLICAÇÃO (MEDIDA DE TRÊS ÂNGULOS IGUAIS). (GIII)

PIERRE VAI FAZER ALGUMAS BANDEIRINHAS PARA SUA FESTA. A FIGURA REPRESENTA O MOLDE DESSA BANDEIRINHA. VEJA, ELA É COMPOSTA POR TRÊS QUADRADOS.

LEMBRANDO QUE O QUADRADO TEM QUATRO ÂNGULOS DE 90⁰, A MEDIDA DO ÃNGULO ASSINALADO NA BANDEIRINHA É IGUAL A:

(A) 90⁰

(B) 135⁰

(C) 180⁰

(D)  270⁰

SARESP/EM

Habilidade Avaliada

H07 - Resolver problemas envolvendo equações do primeiro grau. (GIII)

Jorge emprestou R$ 1.200,00 para seu irmão Gabriel no regime de capitalização simples a uma taxa de 2% ao mês. Ao final de 6 meses, Gabriel saldou sua dívida com jorge. 

Quanto Gabriel pagou para seu irmão Jorge?

(A) R$ 1.344,00

(B) R$ 2.400,00

(C) R$ 2.640,00

(D) R$ 3.600,00

(E) R$ 7.200,00

Cálculo Mental: se 10% corresponde a R$ 120,00, 1% corresponde a R$ 12,00. 

2% corresponde a R$ 12,00 x 2 = R$ 24,00. 

R$ 24,00 x 6 = R$ 144,00.       

R$ 1.200,00 + R$ 144,00 = R$ 1.344,00.

SARESP/Relatório 2010

Habilidade Avaliada – H09 Utilizar a notação científica como forma de representação adequada para números muito grandes ou muito pequenos.

8º.) O diâmetro de um glóbulo vermelho de sangue mede 0,007 milímetros. Esse número, escrito em notação científica, corresponde a:

a)      7 x 10³ milímetros.

b)      7 x 10^-3 milímetros.  

c)      0,7 x 10^-3 milímetros.    

d)      0,7 x 10^-4 milímetros.  

Nível Avançado: ≥ 350.   

SARESP 2014

Exemplo 5²⁹

H03 - Resolver problemas com números racionais que envolvam as operações (adição, subtração, multiplicação, divisão, potenciação e radiciação). 

Estou planejando uma viagem de automóvel. O consumo do veículo é de 10 km/L e o preço do combustível é de R$ 2,00. Se a distância que irei percorrer é de 420 km e o pedágio custa R$ 67,10, o valor que gastarei só para é:

(A)      R$ 96,25.

(B)       R$ 102,75.

(C)       R$ 136,40.

(D)      R$ 151,10.

Percentuais de Acertos: (D) 40,3.

Compõe a descrição do ponto 300 da Escala de Proficiência de Matemática – SARESP

SARESP

https://drive.google.com/file/d/0B65xmAIB-Kr6QW8zUGt2RUprc28/view?usp=sharing